Recursion
A recursive function is a function that calls itself either directly or indirectly through another function. Recursive problem-solving approaches have a number of elements in common. A recursive function is called to solve a problem. The function actually knows how to solve only the simplest cases, or so-called base cases. If the function is called with a base case, the function simply returns a result.
If the function is called with a more complex problem, the function divides the problem into two conceptual pieces: a piece that the function knows how to do and a piece that it does not know how to do. To make recursion feasible, the latter piece must resemble the original problem, but be a slightly simpler or slightly smaller version. Because this new problem looks like the original problem, the function launches (calls) a fresh copy of itself to go to work on the smaller problem this is referred to as a recursive call and is also called the recursion step.
The recursion step also includes the keyword return, because its result will be combined with the portion of the problem the function knew how to solve to form a result that will be passed back to the original caller, possibly main.
The recursion step executes while the original call to the function is still open, i.e., it has not yet finished executing. The recursion step can result in many more such recursive calls, as the function keeps dividing each problem it’s called with into two conceptual pieces. In order for the recursion to terminate, each time the function calls itself with a slightly simpler version of the original problem, this sequence of smaller problems must eventually converge on the base case. At that point, the function recognizes the base case, returns a result to the previous copy of the function, and a sequence of returns ensues all the way up the line until the original call of the function eventually returns the final result to main.
All of this sounds quite exotic compared to the kind of problem-solving we’ve been using with conventional function calls to this point. Indeed, it takes a great deal of practice writing recursive programs before the process will appear natural.
As an example of these concepts at work, let’s write a recursive program to perform a popular mathematical calculation. Recursively Calculating Factorials The factorial of a non-negative integer n, written n! (and pronounced “n factorial”), is the Product n · (n –1) · (n – 2) · … · with 1! equal to 1, and 0! defined to be 1.
For example, 5! is the product 5 * 4 * 3 * 2 * 1, which is equal to 120. The factorial of an integer, number, greater than or equal to 0 can be calculated iteratively (non-recursively) using a for a statement as follows:
factorial = 1;
for ( counter = number; counter >= 1; counter-- )
factorial *= counter;
On the contrary, A recursive definition of the factorial function is arrived at by observing the following relationship:
n! = n · (n – 1)!For example, 5! is clearly equal to 5 * 4! as is shown by the following:
5! = 5 · 4 · 3 · 2 · 1
5! = 5 · (4 · 3 · 2 · 1)
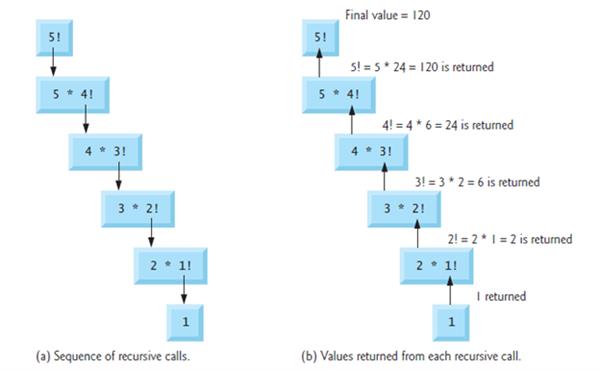
5! = 5 · (4!)The evaluation of 5! would proceed as shown.Example shows how the succession of recursive calls proceeds until 1! is evaluated to be 1, which terminates the recursion. It shows the values returned from each recursive call to its caller until the final value is calculated and returned. It uses recursion to calculate and print the factorials of the integers 0–10 .
The recursive factorial function first tests whether a terminating condition is true, i.e., whether the number is less than or equal to 1. If the number is indeed less than or equal to 1, factorial returns 1, no further recursion is necessary, and the program terminates. If the number is greater than 1, the statement return number * factorial( number - 1 ); expresses the problem as the product of a number and a recursive call to factorial evaluating the factorial of number - 1. The call factorial( number - 1 ) is a slightly simpler problem than the original calculation factorial( number ).
Function factorial has been declared to receive a parameter of type long and return a result of type long. This is shorthand notation for long int. The C standard specifies that a variable of type long int is stored in at least 4 bytes, and thus may hold a value as large as +2147483647. As can be seen in Figure, factorial values become large quickly. We’ve chosen the data type long so the program can calculate factorials greater
Figure
Example
/*Recursive factorial function */
#include <stdio.h>
long factorial( long number ); /* function prototype */
.
/* function main begins program execution */
int main( void )
{
int i; /* counter */
/* loop 11 times; during each iteration, calculate
factorial( i ) and display result */
for ( i = 0; i <= 10; i++ ) {
printf( "%2d! = %ld\n", i, factorial( i ) );
} /* end for */
return 0; /* indicates successful termination */
} /* end main */
/* recursive definition of function factorial */
long factorial( long number )
{
/* base case */
if ( number <= 1 ) {
return 1;
} /* end if */
else { /* recursive step */
return ( number * factorial( number - 1 ) );
}
}
Output :
0! = 1
1! = 1
2! = 2
3! = 6
4! = 24
5! = 120
6! = 720
7! = 5040
8! = 40320
9! = 362880
10! = 3628800than 7! on computers with small (such as 2-byte) integers. The conversion specifier %ld is used to print long values.
Unfortunately, the factorial function produces large values so quickly that even long int does not help us print many factorial values before the size of a long int variable is exceeded.
Forgetting to return a value from a recursive function when one is needed. Either omitting the base cae, or writing the recursion step incorrectly so that it does not converge on the base case, will cause infinite recursion, eventually exhausting memory. This is analogous to the problem of an infinite loop in an iterative (non-recursive) solution. Infinite recursion can also be caused by providing an unexpected input.